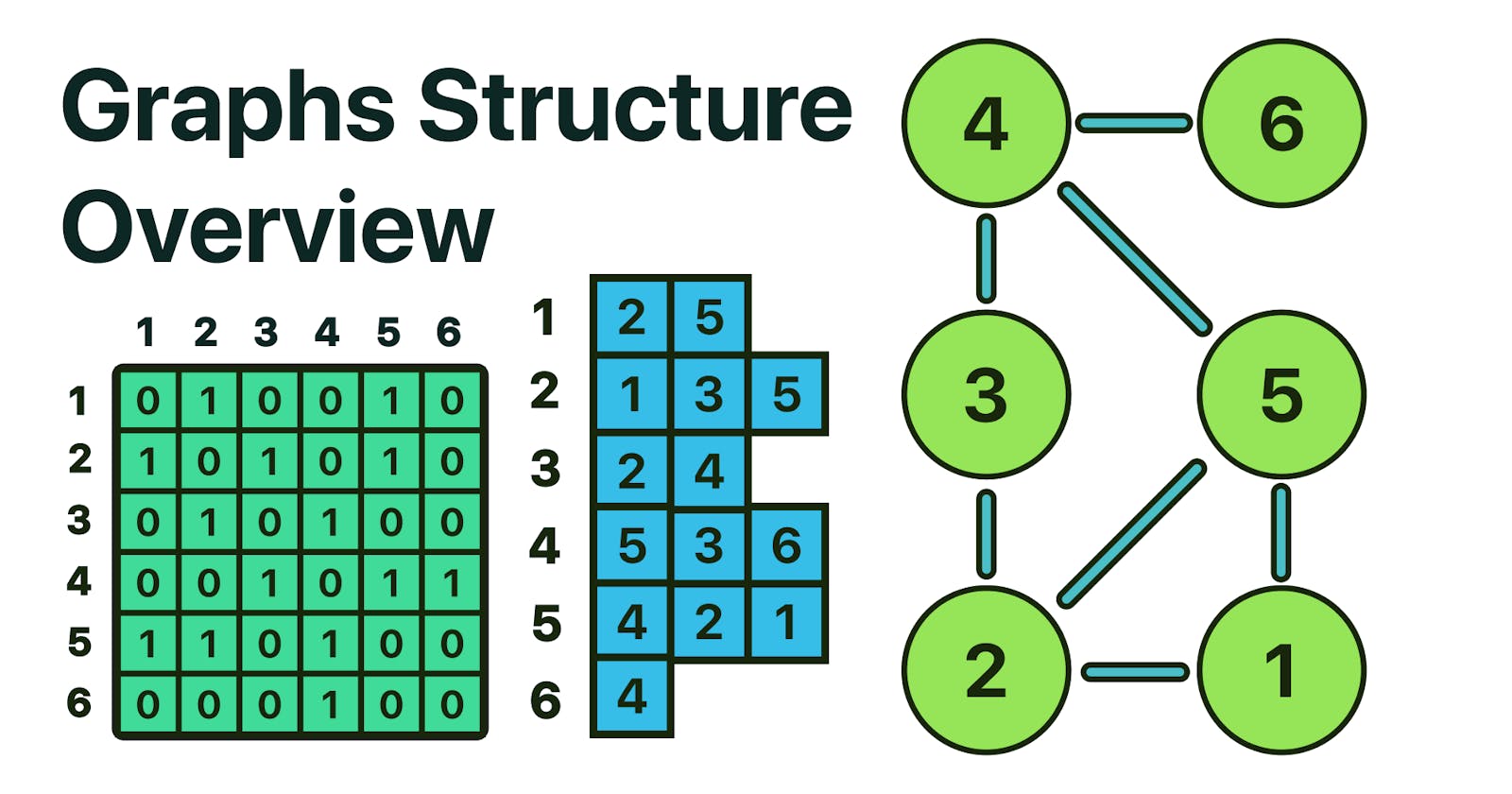
Introduction

Hello everyone! 👋, In this Post, we will take a beginner's dive into Graphs data structure in programming, we'll take a look at what are they, what are they for, the different types of graphs, the differences between graphs and trees, and how to implement a Graph structure using c++,

What is a Graph?

In Computer Science a graph is a non-linear data structure that can be used to represent complex relationships between objects. Graphs are made up of a finite number of nodes or vertices and the edges that connect them. The vertices are sometimes also referred to as nodes and the edges are lines or arcs that connect any two nodes in the graph. In this post, we will follow the node and edge convention.

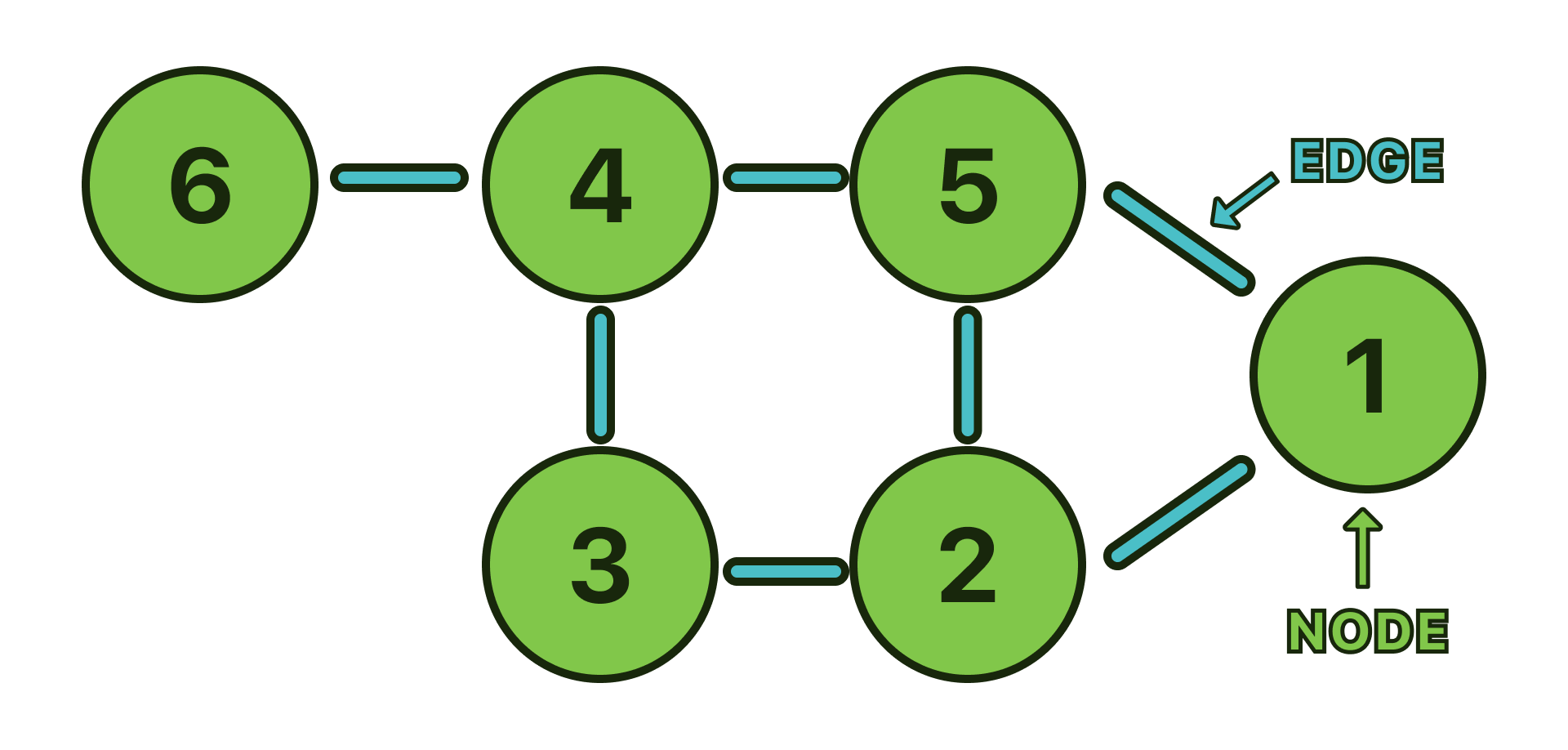
What are Graphs for?

A graph can be a possible choice every time there are relations between objects for example in social networking sites where a user can be represented with a node and connections between them are represented with edges, another good example can be found on google maps where a location can be represented as the node, and the path can be represented with the edges, then we can implement an algorithm to find the shortest route between two nodes. Graphs can also be used for solving puzzles with only one solution like mazes.

Types Of Graph

1. Null Graph - There are no edges connecting the Nodes.

2. Trivial Graph - only has one single node and it's the smallest graph possible.

3. Undirected Graph - Edges don't have any direction, if a node A connects a node B the opposite is true.

4. Directed Graph - All edges have a specified direction, the normal convention is that node A connects the node B in that order.

5. Connected Graph - Each one of the nodes can visit any other node in the Graph.

6. Disconnected Graph - If at least one node is not reachable from another node is considered a disconnected Graph.

7. Complete Graph - Every single node is connected to each other node.

8. Cycle Graph - A graph where all of the nodes form one perfect cycle.

9. Cyclic Graph - at least 1 cycle is formed within the Graph.

10. Bipartite Graph - A graph in which the nodes can be divided into two sets such that the nodes in each set do not contain any edge between them.

11. Weighted Graph - A graph where all of its edges have a specified value, for example, if each node represents a city, the edges can represent roads with the time it takes to reach another city.

Basic Operations for Graphs

Here are some of the most common and basic operations for Graphs:

• Insertion of Nodes/Edges
• Deletion of Nodes/Edges
• Searching - Uses Algorithms like BFS
• Traversal - Visit all the nodes in the graph using algorithms like DFS

Tree vs Graph

If you have worked with trees before, you might get a little confused about the differences, but in simple terms, just know that trees are just more restricted types of graphs. Every tree is always a graph, but not every graph is a tree. The same is true with Linked Lists and Heaps.

Representing a Graph

You might be wondering how can a graph be represented with code. Well, there are 2 simple ways to store a graph, using an Adjacency Matrix or an Adjacency List, we'll see both of them in action.

Adjacency Matrix

In this method, the graph is stored in the form of a 2D matrix where rows and columns denote the nodes and each entry in the matrix represents either 1(connected) or 0(disconnected), if the graph you are trying to represent is a weighted graph, then you can put the weight instead.

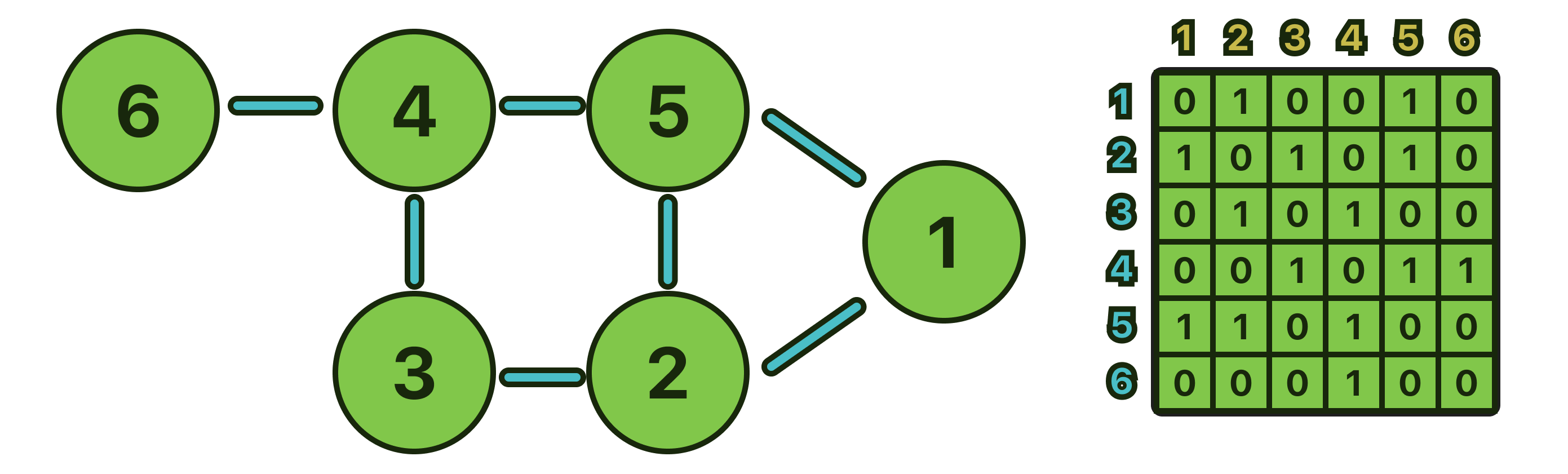
In the image above, you can see how that specific graph would be represented using an adjacency matrix, the node 1 is connected to nodes 2 and 5, that's why on row 1 columns 2 and 5 are 1 which means connected, this process repeats for every single node.

Adjacency List

This method is very similar to the 2D matrix because we are going to create a collection of N empty lists, and for each node, we push_back() the adjacent nodes like this:

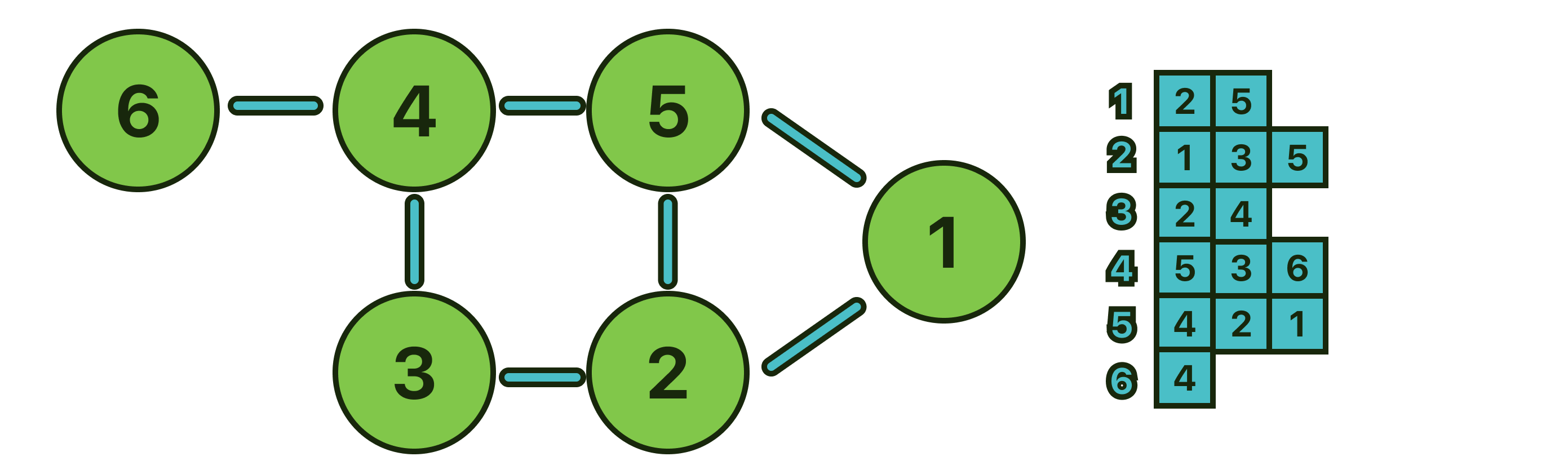
If you want to use this method to represent a weighted graph then you would have to save pairs in each element of the array, the node, and the weight.

Differences Between Methods.

there are several factors to consider when choosing what method to use. If for example, the amount of nodes N is very large, then you only have the adjacency list method which in most cases has way less memory usage, however, the Matrix method can perform O(1) constant operation for adding a node as well as for removing a connection which the adjacency list does not. However, if we try to consult the adjacent nodes to a specific node the List method is better since it doesn't have unnecessary nodes stored in it, and on top of that, you can be more creative by ordering the list or changing the List for a priority queue, set, and more.

Implement a Graph Structure in C++

Receiving Input

The problem normally specifies how the input is given, but the standard is as follows: In the first line N and K where N is the number of nodes in the graph and K is the number of edges, then we are given K lines, and for each line A and B representing that the node A connects node B, the problem normally specifies if it's directed or undirected and if it's a weighted graph, if it is, the third number for each line is added representing the weight of the edge.

Adjacency Matrix

The code below uses a 2D vector of booleans because, for this particular example, the graph is Undirected and has no weight.

#include <iostream>
#include <vector>

using namespace std;

int main() {
  int n, k;
  cin >> n >> k;
  // +1 because the graph nodes start from 1 not 0
  vector<vector<bool>> GRAPH(n + 1, vector<bool>(n + 1)); 
  for (int i = 0; i < k; i++) {
    int nodeA, nodeB;
    cin >> nodeA >> nodeB;
    GRAPH[nodeA][nodeB] = 1;
    GRAPH[nodeB][nodeA] = 1;
  }
  for (auto row : GRAPH) {
    for (auto col : row) cout << col << " ";
    cout << endl;
  }
  return 0;
}

Remember that if we wanted to represent a weighted graph, we receive an extra parameter for every edge, normally at the end, with the weight of that connection, and the only thing we would have to do is change the bool for int on our matrix.

If the problem specifies that the graph is directed, we would have to simply remove: GRAPH[nodeB][nodeA] = 1; and that's it!

Adjacency List

In the code cell below you can see the implementation. Notice how it's very similar to the Matrix method.

#include <iostream>
#include <vector>

using namespace std;

int main() {
  int n, k;
  cin >> n >> k;
  // +1 because the graph nodes start from 1 not 0
  vector<vector<int>> GRAPH(n + 1);
  for (int i = 0; i < k; i++) {
    int nodeA, nodeB;
    cin >> nodeA >> nodeB;
    GRAPH[nodeA].push_back(nodeB);
    GRAPH[nodeB].push_back(nodeA);
  }
  for (int node = 1; node <= n; node++) {
    cout << node << " : ";
    for (auto adjacent : GRAPH[node]) cout << adjacent << ", ";
    cout << endl;
  }
  return 0;
}

I personally like this method more because we are saving a lot of memory and it's more readable and easy to understand in my opinion. Remember that if we wanted to add weight to this graph, instead of doing: .push_back(nodeB); we can: .push_back({nodeB, weight}); and change the vector type from int, to pair.

Conclution - Farewell

You've reached the end of this lesson on Graphs, remember that this is a skill that takes a lifetime to master so don't feel frustrated if you don't get it right away because this isn't easy, but I really hope some of the guidelines we saw today were helpful and the basic foundations on this topic were well understood, remember, there is still a lot to learn and we definitively didn't cover everything on Graphs, but I hope this was a good beginner overview and that you managed to grasp the basic ideas.

Let me know in the comments what you thought about this post and let me know what you will like to see next. In the next posts, we are going to dive a little bit more into this topic and we will see the common algorithms that are applied to Graphs, like DFS and BFS, and how we can use them to solve some basic competitive programming problems. Stay tuned!