Introduction

Hello everyone 👋, In today's post I wanted to talk about the famous Dijkstra algorithm, we are going to see what it is, what it's used for, how it works, and the implementation of the algorithm in c++ altho the idea can be applied in any language.

Before we continue I highly recommend you read the following resources:

• Graphs Introduction For Beginners

• BFS and DFS Beginners Overview

What is Dijkstra?

The Dijkstra algorithm is a graph search algorithm that solves the single-source shortest path problem for a graph with non-negative edge weights, producing a shortest path tree, this means that we can know the shortest distance from the origin node to the rest of the nodes in a graph. It is very similar to the BFS algorithm, however, the BFS algorithm does not give the shortest distance in a weighted graph.

What is Dijkstra Used For?

Dijkstra's algorithm is a popular choice for finding the shortest path in a graph, and it has many practical applications. Some examples of where Dijkstra's algorithm is used include:

1. Navigation: Dijkstra's algorithm can be used to find the shortest route between two locations on a map, taking into account factors such as distance, time, and traffic.

2. Network routing: In computer networking, Dijkstra's algorithm can be used to find the shortest path between two nodes in a network, such as routers or servers.

3. Traffic management: Dijkstra's algorithm can be used to optimize traffic flow by finding the shortest routes for vehicles to take, based on factors such as distance, time, and traffic.

4. Resource allocation: Dijkstra's algorithm can be used to find the most efficient allocation of resources, such as in a supply chain or manufacturing process.

5. Artificial intelligence: In artificial intelligence and machine learning, Dijkstra's algorithm can be used to find the shortest path in a graph representing a problem space, such as in pathfinding or planning.

These are just some examples, in my case I use Dijkstra for competitive programming problems, we'll look at an example later in this post.

How Does The Algorithm Work?

The Dijkstra algorithm works by starting from a specified node and repeatedly expanding to the closest adjacent node until it reaches the destination node, very similar to the BFS algorithm however the Dijkstra algorithm uses a priority queue instead of a queue, this is necessary since the adjacent node with the less cost has the highest priority. At each step, the algorithm removes the node at the front of the priority queue and updates the distances of its adjacent nodes based on the distance from the starting node to the current node.

To implement Dijkstra's algorithm, we need to keep track of the following information for each node:

• The distance from the starting node to the current node.

• The previous node in the path from the starting node to the current node.

Initially, the distance of the starting node is set to 0, and the distances of all other nodes are set to infinity. As the algorithm progresses, it updates the distances of the neighboring nodes based on the distance from the starting node to the current node.

Here is an outline of the steps:

1. Set the distance of the starting node to 0 and the distance of all other nodes to infinity.

2. Add the starting node to the priority queue

3. While the priority queue is not empty:

   1. Remove the node with the highest priority (lowest distance) from the priority queue, (The Top).

   2. Check if the current node has a cost greater than what it already has, if this is true, it means that the cost is not being improved and we can continue .

   3. Update the distances of its neighboring nodes based on the distance from the current node to the neighboring node.

   4. Save that the neighboring node comes from the current node in the BACK array, this is going to help us to recreate the path.

   5. Add the neighboring nodes to the priority queue.

4. Once the priority queue is empty, we can reconstruct the shortest path from the starting node to the destination node by following the previous nodes back from the destination node to the starting node using the BACK.

This algorithm is more efficient and can handle larger graphs in comparison to other algorithms like the "Bellman-Ford". However, the Dijkstra algorithm requires that there are no negative weight edges.

Example - Visualization

In order to better understand the algorithm I made the following animation:

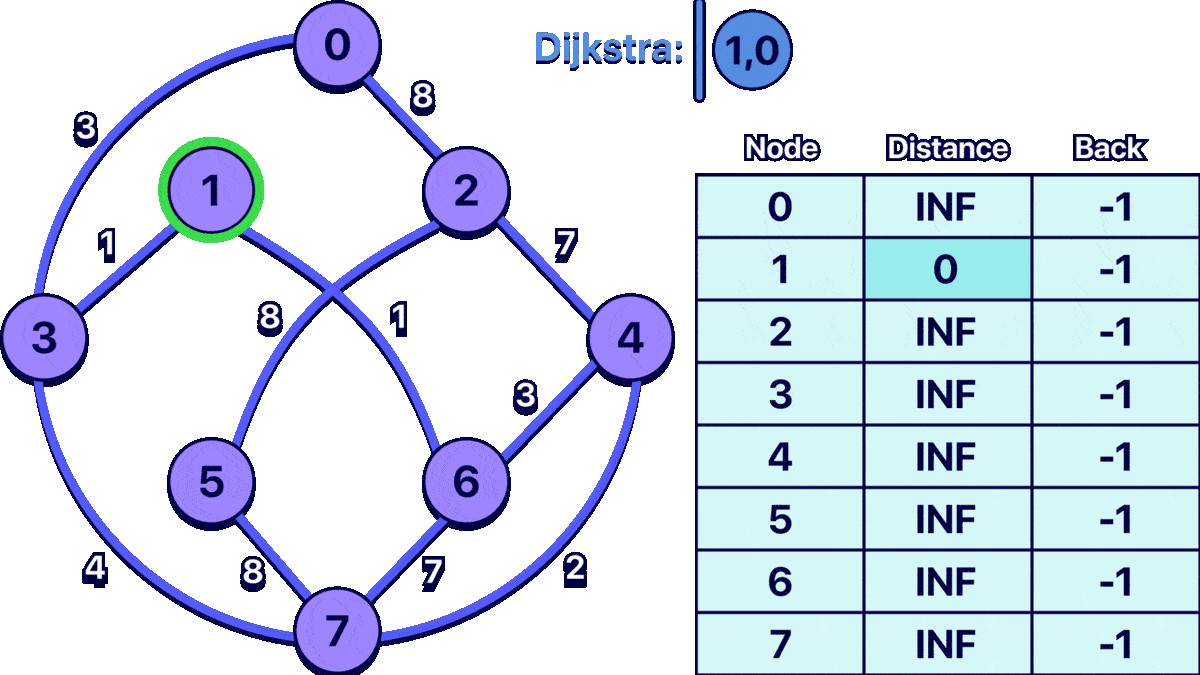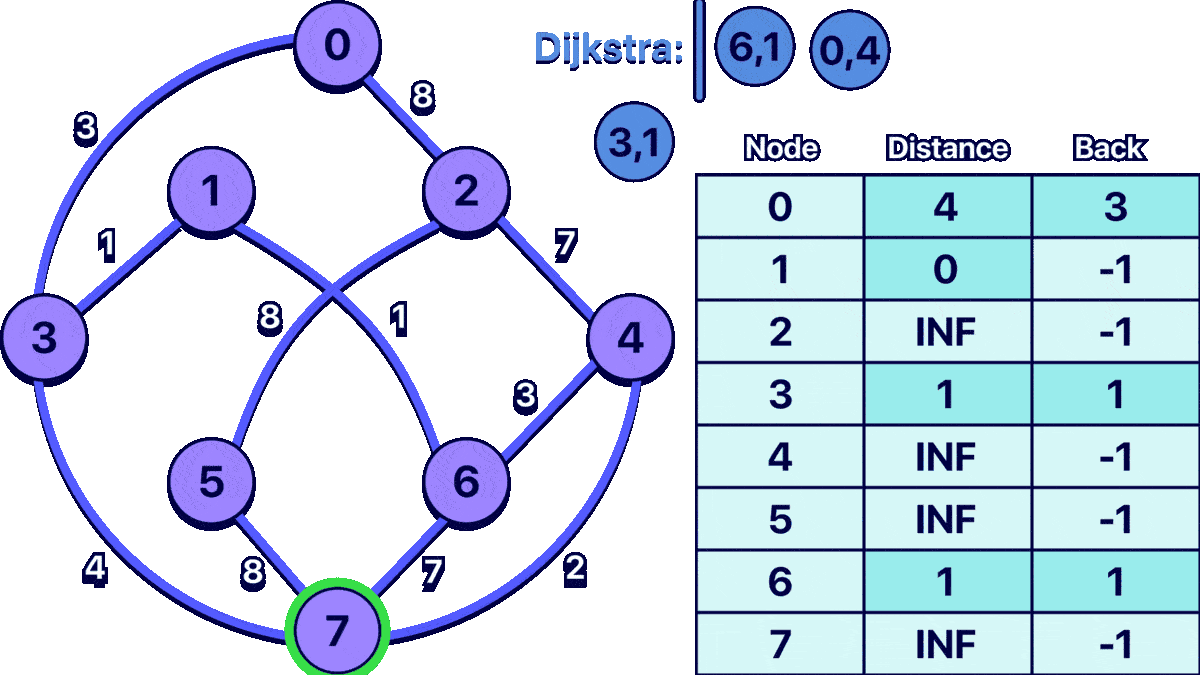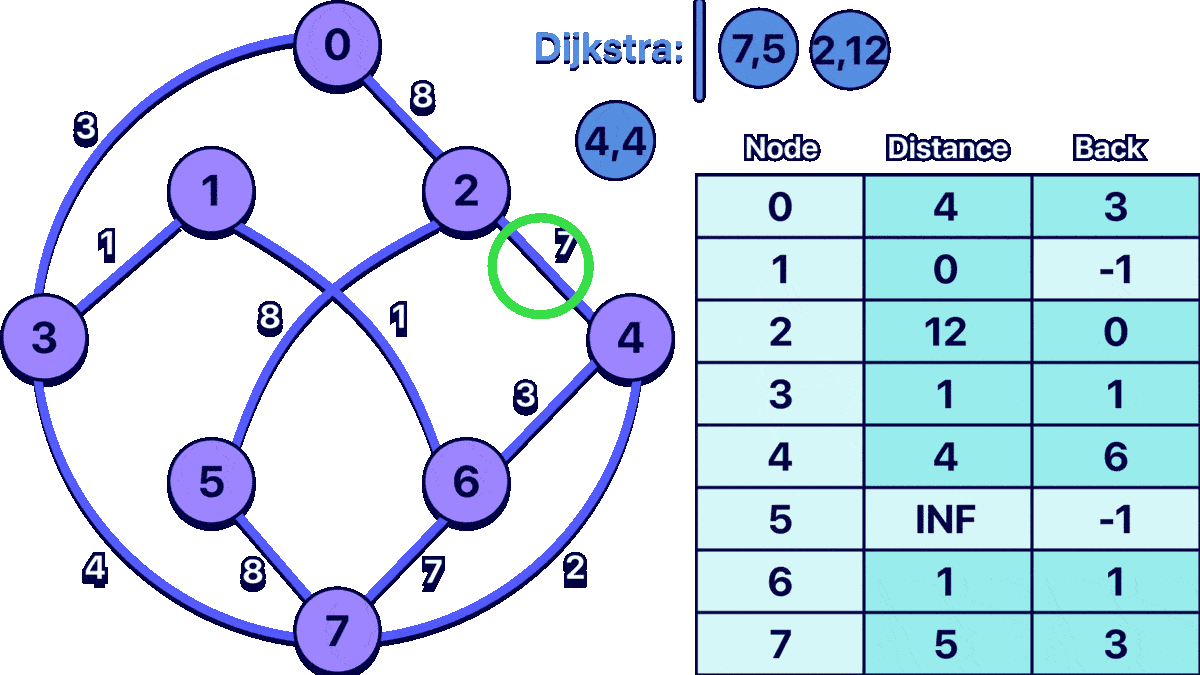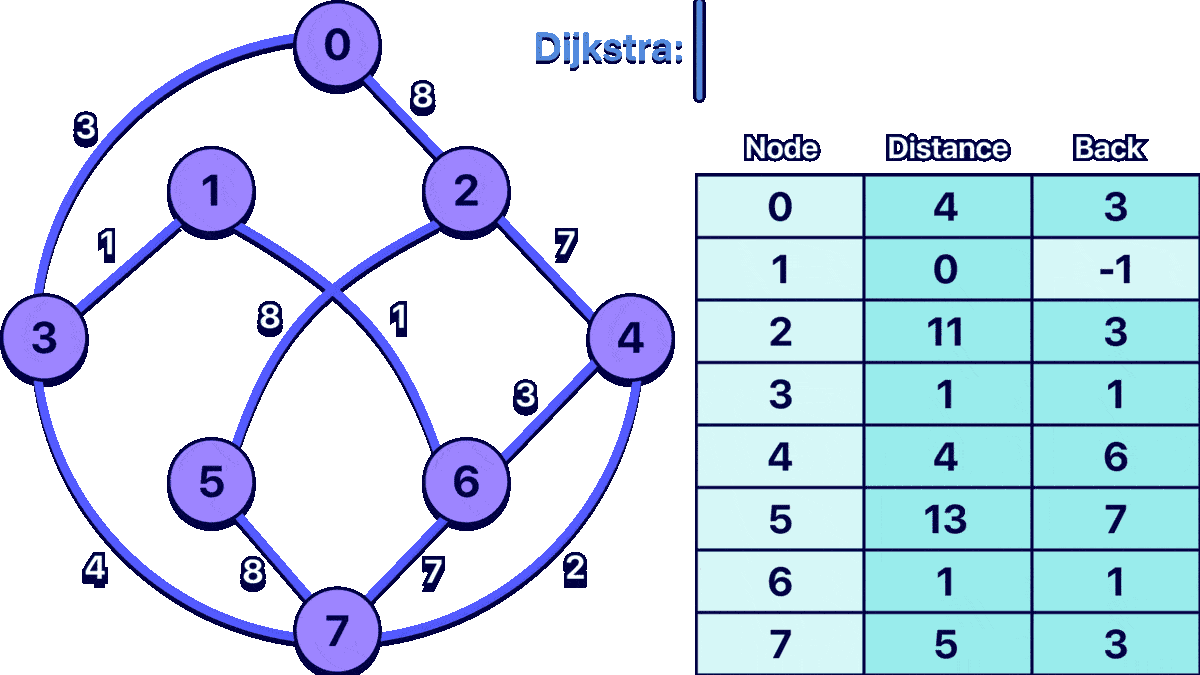
the input for the example graph shown above would be:

8 11
0 3 3
0 2 8
1 3 1
1 6 1
2 5 8
2 4 7
3 7 4
4 7 2
4 6 3
5 7 8
6 7 7
1

The last number is the starting node.

Code Implementation

Below you can find the implementation of the algorithm in c++, remember that there are several ways to code this algorithm and I'm just showing the version I use. you can find the explanation below the code cell.

#include<iostream>
#include<vector>
#include<queue>
#include<algorithm>
using namespace std;
typedef long long ll;

struct node{
    int node;
    ll cost;
    bool operator < (const struct node &b) const{
        if(cost != b.cost) return cost > b.cost;
        if(node != b.node) return node > b.node;
        return 0;
    }
};

const ll INF = 1E18;

int main(){
    int n, m; cin>>n>>m;
    vector<vector<node>> adj(n);
    vector<int> BACK(n, -1);

    for(int i = 0; i < m; i++){
        int u, v; ll w;
        cin>>u>>v>>w;
        adj[u].push_back({v, w});
        adj[v].push_back({u, w});
    }

    vector<ll> dist(n, INF);
    int source; cin >> source;
    dist[source] = 0;

    priority_queue<node> dijkstra;
    dijkstra.push({source, 0});

    while(!dijkstra.empty()){
        node c = dijkstra.top();
        dijkstra.pop();
        if(c.cost > dist[c.node]) continue;

        for(node adj: adj[c.node]){
            if(c.cost + adj.cost >= dist[adj.node])continue;
            dist[adj.node] = c.cost + adj.cost;
            BACK[adj.node] = c.node;
            dijkstra.push({adj.node,c.cost + adj.cost});
        }
    }

    for(int i = 0; i < n; i++){
        cout<<i<<": cost:"<<dist[i]<<" path:";
        vector<int> path;
        int current = i;
        while (current != -1) {
            path.push_back(current);
            current = BACK[current];
        }
        reverse(path.begin(), path.end());
        for(auto e:path)cout << e << " ==> ";
        cout << endl;
    }

    return 0;
}

First, we define our node struct, which is going to have two properties, the name or in this case number of the node, and the cost or weight. Notice that we also define the "<" operator, this is necessary and very important for the priority queue to know how to order the nodes by cost. Then we input the graph itself in the exact same way as we do with a BFS algorithm and we set the source distance to 0. Notice how we are going to keep track of the distances in the dist vector. Additionally, we also define the Back vector, with -1 as the default value.

Now we define our Priority Queue which I like to call "Dijkstra" and we push the origin node while it's not empty, we are going to perform the following actions:

remove the top of the priority queue. Check if the node has a cost greater than the already saved distance for that node in the dist vector, in which case you continue.

if(c.cost > dist[c.node]) continue;

This is going to help to not come back from where you came from. Else, we are going to iterate through the adjacent nodes to that node and once again check if the distance from the current node plus the neighboring node improves the cost. If it is greater, that means worse so continue.

if(c.cost + adj.cost >= dist[adj.node])continue;

else we update the distance to that adjacent node, the back, and push that adjacent node with the updated cost.

dist[adj.node] = c.cost + adj.cost;
BACK[adj.node] = c.node;
dijkstra.push({adj.node,c.cost + adj.cost});

Once the Dijkstra is empty, we can prove that it worked by showing the minimum cost from the origin to the rest of the nodes, AND the path that it took.

for(int i = 0; i < n; i++){
    cout<<i<<": cost:"<<dist[i]<<" path:";
    vector<int> path;
    int current = i;
    while (current != -1) {
        path.push_back(current);
        current = BACK[current];
    }
    reverse(path.begin(), path.end());
    for(auto e:path)cout << e << " ==> ";
    cout << endl;
}

The process to recover the path is exactly the same as with the BFS.

Now you can try to run the full code with the example input and you should get the following output:

0: cost:4 path:1 ==> 3 ==> 0 ==> 
1: cost:0 path:1 ==> 
2: cost:11 path:1 ==> 6 ==> 4 ==> 2 ==> 
3: cost:1 path:1 ==> 3 ==> 
4: cost:4 path:1 ==> 6 ==> 4 ==> 
5: cost:13 path:1 ==> 3 ==> 7 ==> 5 ==> 
6: cost:1 path:1 ==> 6 ==> 
7: cost:5 path:1 ==> 3 ==> 7 ==>

Conclusion - Farewell

In conclusion, the Dijkstra algorithm is a powerful tool for finding the shortest path between two nodes in a graph. Whether you are a beginner or an experienced programmer, understanding how the Dijkstra algorithm works is an important skill to have in your toolkit. Whether you are navigating a map, routing network traffic, or optimizing the allocation of resources, the Dijkstra algorithm can help you find the most efficient solution to a wide range of problems. So if you want to learn more about the Dijkstra algorithm and how to implement it in your own projects, be sure to check out the resources and code samples provided in this post.

remember that this is a skill that takes a lifetime to master so don't feel frustrated if you don't get it right away because this isn't easy, but I hope some of the guidelines we saw today were helpful and the basic foundations on this topic were well understood, remember, there is still a lot to learn and we definitively didn't cover everything on Dijkstra, but I hope this was a good beginner overview and that you managed to grasp the basic ideas.

Let me know in the comments what you thought about this post and let me know what you will like to see next. Stay tuned!